[알고리즘] 합병 정렬(Merge Sort)

Goal

Merge Sort 알고리즘을 이해한다.
Merge Sort 알고리즘의 특징
Merge Sort 알고리즘의 시간 복잡도
Merge Sort 알고리즘을 C언어로 구현한다.

Merge Sort 알고리즘 개념 요약

• 분할 정복 (Divide and Conquer) 알고리즘의 하나이다.

• 분할 정복 알고리즘은 대게 Recursion을 활용하여 구현한다.

• 간단한 과정 설명

  • 배열의 길이가 0 또는 1이면 이미 정렬이 다 된것으로 본다.
  • 정렬되지 않은 배열을 반으로 잘라 두개의 배열로 나눈다.
  • 각 배열을 재귀적으로(Recursion) 다시 Merge Sort를 이용해 정렬한다.
  • 정렬된 모든 배열을 다시 하나의 배열로 Merge 해준다.

Merge Sort 알고리즘 구체적 개념

• 하나의 배열을 두 개의 균등한 크기로 분할하고 분할 된 배열을 정렬한 다음, 두개의 정렬 된 배열을 다시 합하여 최종적으로 정렬된 리스트가 되게 하는 알고리즘 이다.

• Merge Sort는 다음과 같은 단계들로 이루어진다.

  • 분할(Divide) : 배열을 같은 크기의 부분 배열 2개로 분할한다.
  • 정복(Conquer) : 부분 배열을 정렬한다. 부분 배열의 크기가 1 또는 0이 아닐때는 Recursion을 활용해 Divide를 다시 한다.
  • 결합(Combine) : 정렬된 부분배열들을 다시 하나의 배열로 결합한다.

Merge Sort 알고리즘 예제

Ⅰ. 배열에 21, 10, 12, 20, 25, 13, 15, 22가 들어있다고 보고 이를 Merge Sort해보자
Ⅱ. 먼저 배열을 두개로 쪼개어 나눈다 (Divide)
Ⅲ. 배열의 원소 개수가 1개가 될때 까지 계속 나눈다 (Divide)
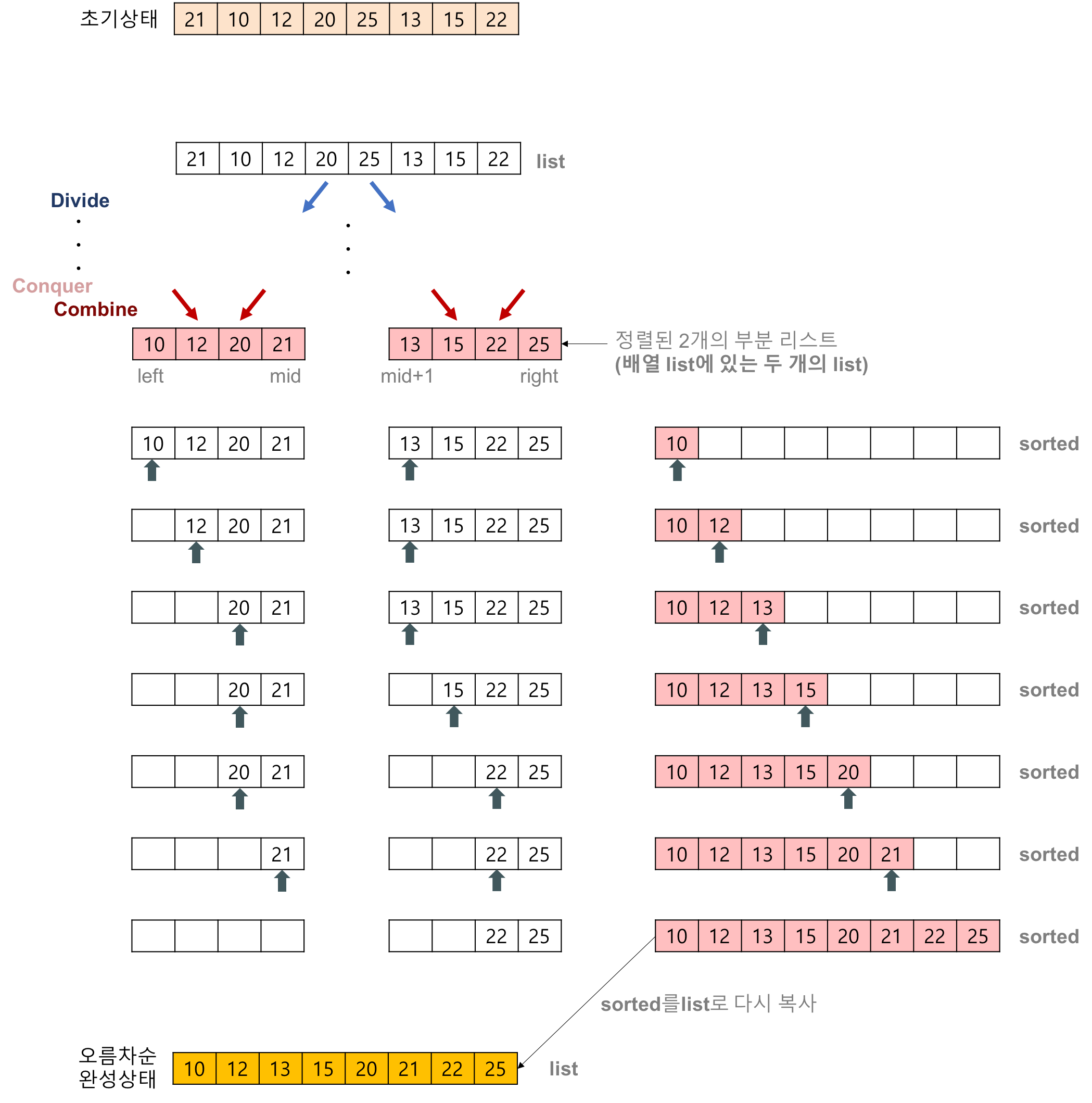
Ⅳ. 나뉜 배열을 두개씩 비교해 정렬하고 합친다 ( Conquer & Combine )
Ⅴ. 합치는 과정을 반복해 최종적으로 정렬된 배열을 찾는다.

Merge Sort 알고리즘 과정

Merge Sort 코드

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

// i = 정렬된 왼쪽 배열의 인덱스
// j = 정렬된 오른쪽 배열의 인덱스
// k = 최종 정렬된 배열의 인덱스
void merge(int* arr, int left, int mid, int right) {

	int* temp = (int*)malloc(sizeof(int) * (right - left + 1));
	int i = left;
	int j = mid + 1;
	int k = 0;

	while (i <= mid && j <= right) {
		if (arr[i] <= arr[j]) temp[k++] = arr[i++];
		else temp[k++] = arr[j++];
	}

	while (i <= mid) temp[k++] = arr[i++];

	while (j <= right) temp[k++] = arr[j++];

	i = left;
	k = 0;

	while (i <= right) arr[i++] = temp[k++];

	free(temp);
}


void mergeSort(int* arr, int left, int right) {
	if (left < right) {
		int mid = (left + right) / 2;
		mergeSort(arr, left, mid);
		mergeSort(arr, mid + 1, right);
		merge(arr, left, mid, right);
	}
}


int main() {
	int n = 0;
	scanf("%d", &n);

	int* pArr = (int*)malloc(sizeof(int) * n);

	for (int i = 0; i < n; i++) {
		scanf("%d", &pArr[i]);
	}

	// 배열 시작부터 끝까지 mergesort실행
	mergeSort(pArr, 0, n - 1);

	for (int i = 0; i < n; i++) {
		printf("%d\n", pArr[i]);
	}

	free(pArr);
	return 0;
}