[머신러닝] [Python] 1. Decision Trees (결정 트리)

Decision Tree란

Decision Tree (결정 트리, 의사결정트리, 의사결정나무) 는 분류(Classification)와 회귀(Regression)이 모두 가능한 지도 학습 모델(Supervised Learning) 중 하나이다. 이러한 특성 때문에 CART(Classification and Regression Tree) 알고리즘의 하나이기도 하다. 결정 트리는 예/아니오 질문을 이어가며 학습하는데 예를 들어 매, 펭귄, 돌고래, 곰을 구분한다고 보자. 매와 펭귄은 날개가 있고, 돌고래와 곰은 날개가 없다. 날개가 있나요? 라는 질문을 통해 매, 펭귄 / 돌고래, 곰 으로 집단을 나눌 수 있다. 매와 펭귄은 날 수 있나요? 라는 질문을 통해 매 / 펭귄으로 나눌 수 있고 돌고래와 곰은 지느러미가 있나요? 라는 질문을 통해 나눌 수 있다.

이렇게 특정 기준에 따라 데이터를 구분하는 모델을 트리 모델이라고 한다. 한번의 분기마다 영역을 여러개로 나누고 이때 기준 하나하나를 노드(Node)라고 한다. 맨 처음 분류 기준을 Root Node라고 하며 맨 마지막 노드를 Leaf Node라고 한다.

트리를 어떻게 나눌까?

트리구조를 만들기 위해서는 고려해야할 사항이 몇가지 있다.

1. 데이터를 나누는 기준

2. Determine the Best Split

크게 보면 이렇게 두가지 인데 먼저 첫번째 고려사항부터 살펴보자.

1. 데이터를 나누는 기준

---

데이터를 나누는 기준은 1. 데이터 타입과 2. 나눌 가짓수 에 따라 나눈다.

• 1.데이터 타입
  • Categorical attribute ( 문자 )
    • nominal attribute ( 순서가 없는 데이터)
    • ordinal attribute ( 순서가 있는 데이터 ex) “S, M, L, XL” )
  • Continuous arrtibute ( 숫자 )
    • Discretization (이산화)
    • Binary Decision

• 2.나눌 가짓수
  • 2-way split
  • multi-way split

2. Determine the Best Split

종류가 같은 / 비슷한 class로 분배하는것이 가장 적절하다. 여기서 class란 target과 같은 의미이다. 이는 데이터의 impurity가 낮다는것을 의미한다.

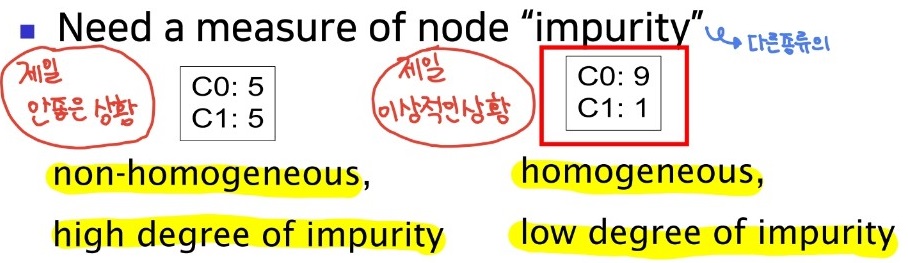
노드의 Impurity(불순도)

1. Entropy

불순도를 수치화한 지표 중 하나이며 엔트로피의 값에 따라 Decision Tree의 분류가 일어난다.

Entropy가 0일 경우, 개체의 속성이 모두 동일하다. 즉 분류가 필요없다.

Entropy가 1에 가까울 경우, 불순도가 높다.

Entropy가 0에 가까울 경우, 불순도가 낮다.

한마디로 Impurity와 Entropy는 비례관계라고 볼 수 있다.

엔트로피의 계산공식은 아래와 같다.

2. Gini Index ( 지니계수 )

불순도를 측정하는 지표로 통계적 분산정도를 정량화하여 표현한 값이다.

지니계수가 클수록 데이터가 equally distributed, 즉 비효율적으로 분산된것이고 지니계수가 작을수록 데이터가 가장 이상적으로 분산된 것을 의미한다.

지니계수의 계산은 아래 그림과 같다.

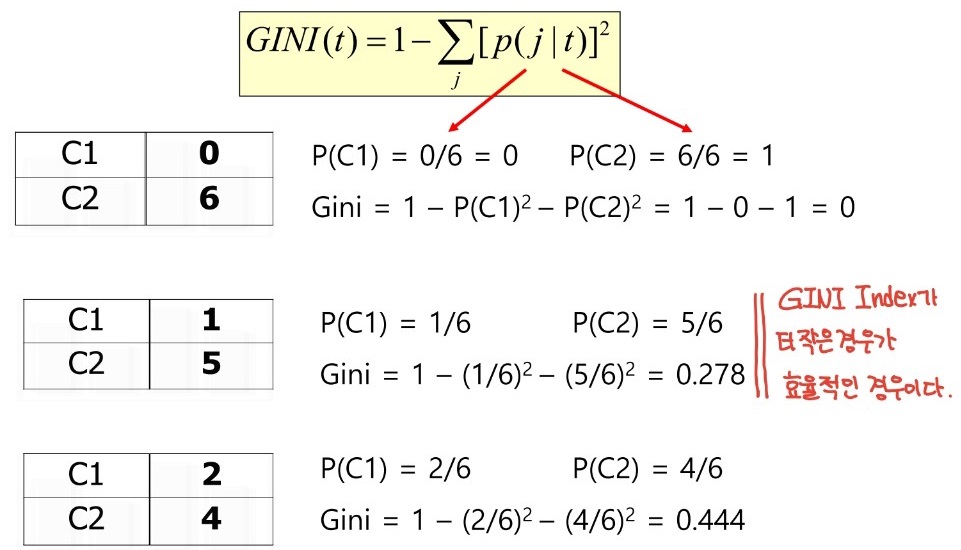
※ 그렇다면 Gini Index를 이용해서 Split의 기준을 정할 때 아래 그림처럼 Gini Index를 비교하는 방법을 무엇일까?

A와 B 둘중 어떤 것이 더 잘 분기된것인지를 알기 위해선 Gini Gain을 활용해야 한다.

2-1. Gini Gain

Gini Gain은 각 데이터의 Gini Index를 비교하기 위한 수치이다.

좀 더 쉬운 이해를 위해 예제와 함께 살펴보자.

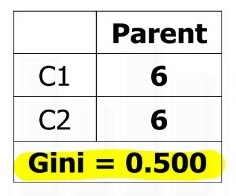
분기 이전 원래 데이터의 Gini 계수 : Gini(Parent) = 1 - (6/12)² - (6/12)² = 0.5

N1의 Gini 계수 : Gini(N1) = 1 - (5/7)² - (2/7)² = 0.41

N2의 Gini 계수 : Gini(N2) = 1 - (1/5)² - (4/5)² = 0.32

Gini Gain을 활용한 분기 이후 Gini 계수 : Gini(children) = 7/12 x 0.41 + 5/12 x 0.32 = 0.372

3. Classification Error (분류 오차)

지니계수와 거의 비슷하지만 조금더 단순하고 간단하다. 어려운 내용은 아니니 예제로 바로 설명해보겠다.

C1과 C2의 Error값을 각각 계산해주고 둘중 더 큰값을 1에서 빼주면 되는 간단한 수식이다.

Classification Error는 간단하게 계산 가능하다는 장점이 있지만 Gini Index보다는 Impurity를 판단하는 정확도가 떨어진다는 단점이 있다.